Формула дискримінанту – що це таке та як її використовувати?

Що таке формула дискримінанту?

Формула дискримінанту використовується в математиці для визначення кількості коренів квадратного рівняння. Вона є важливою складовою розв’язку рівнянь виду .

Формула дискримінанту у квадратному рівнянні

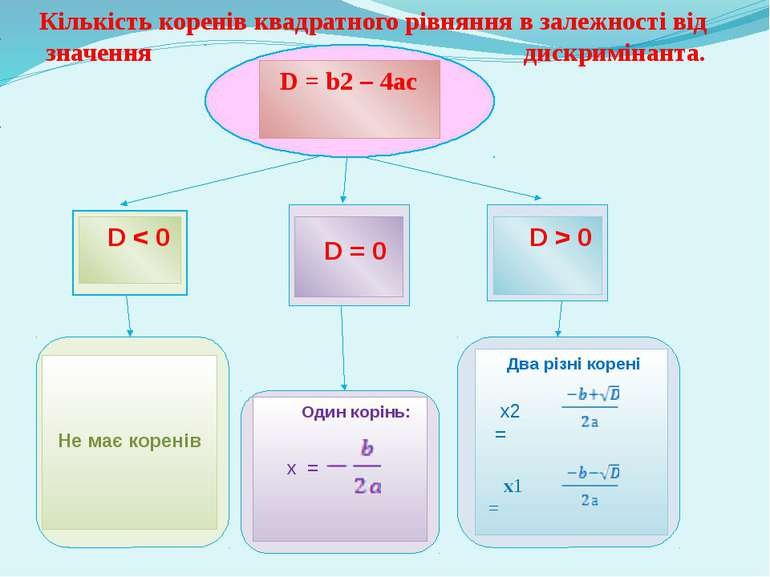
Для квадратного рівняння дискримінант позначається буквою і обчислюється за формулою:

Де:

• , , — коефіцієнти рівняння.

Як визначити кількість коренів за формулою дискримінанту?

Результат обчислення дискримінанту допомагає зрозуміти, скільки коренів має рівняння:

• Якщо , рівняння має два різних корені.
• Якщо , рівняння має один корінь (подвійний).
• Якщо , рівняння не має дійсних коренів.

Як знайти корені рівняння за допомогою дискримінанту?

Якщо , корені квадратного рівняння можна знайти за формулою:

Приклад розв’язку квадратного рівняння

Розглянемо рівняння:

1. Обчислимо дискримінант:
2. Оскільки , рівняння має два різних корені:

Отже, розв’язок: .

Чому формула дискримінантуу важлива?

Формула дискримінантуу допомагає швидко визначити, чи має рівняння розв’язки, що дуже корисно при розв’язуванні математичних задач.

Формула дискримінантуу в реальному житті

Квадратні рівняння зустрічаються у фізиці, економіці та навіть у будівництві. Наприклад, вони допомагають знаходити оптимальні розміри конструкцій або аналізувати фінансові моделі.

Поширені помилки при використанні формули дискримінанту

1. Неправильний розрахунок значення .
2. Забуття про знак при обчисленні коренів.
3. Використання формули, коли рівняння не є квадратним.

Висновок

Формула дискримінанту — це ключовий інструмент для розв’язку квадратних рівнянь. Вона дозволяє швидко визначити, скільки коренів має рівняння, а також знайти їх значення.

Читати далі: Синтаксичний розбір речення: Покрокова Інструкція та Приклади

Поширені запитання