Площа паралелограма — це одна з найважливіших тем у геометрії, адже вона часто зустрічається у завданнях. Вона допомагає зрозуміти, як працюють площини та фігури у просторі. Щоб правильно розрахувати площу паралелограма, потрібно знати формули, властивості та вміти застосовувати їх на практиці.
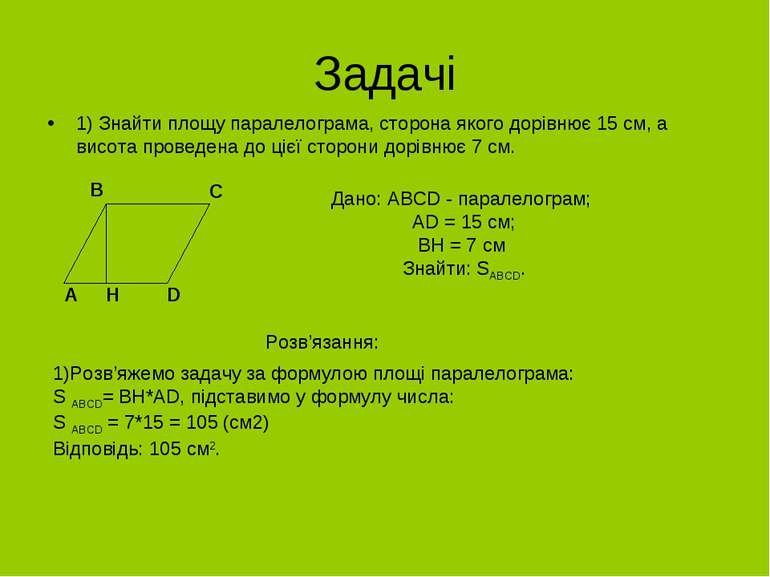
Що таке площа паралелограма
Площа паралелограма — це числове значення, яке показує, скільки простору займає ця фігура на площині. Іншими словами, вона відображає розмір поверхні, обмеженої сторонами паралелограма.
Властивості паралелограма і їх роль у знаходженні площі
Паралелограм має кілька важливих властивостей, які впливають на обчислення його площі. Протилежні сторони рівні, протилежні кути однакові, а діагоналі перетинаються та діляться навпіл. Завдяки цим властивостям можна застосовувати різні формули для знаходження площі.
Формула площі паралелограма через основу і висоту
Найпростіший спосіб обчислити площу паралелограма — використати основу та висоту:
S = a × h
де:
- a — довжина основи,
- h — висота, проведена до цієї основи.
Приклад обчислення площі паралелограма через основу і висоту
Якщо основа паралелограма дорівнює 8 см, а висота, проведена до цієї основи, становить 5 см, тоді:
S = 8 × 5 = 40 см²
Формула площі паралелограма через сторони та синус кута
Інколи висоту невідомо, тоді використовують іншу формулу:
S = a × b × sin(α)
де:
- a, b — довжини сусідніх сторін,
- α — кут між ними.
Приклад використання формули із синусом
Нехай сторони паралелограма мають довжини 10 см і 6 см, а кут між ними дорівнює 30°. Тоді:
S = 10 × 6 × sin(30°) = 10 × 6 × 0.5 = 30 см²
Площа паралелограма через діагоналі і кут між ними
Ще одна формула допомагає тоді, коли відомі діагоналі:
S = (d₁ × d₂ × sin(α)) / 2
де:
- d₁, d₂ — діагоналі,
- α — кут між ними.
Геометричний зміст площі паралелограма
Площа паралелограма відображає, скільки квадратних одиниць міститься в його межах. Це означає, що ми можемо накрити його квадратами однакового розміру й отримати точне значення.
Використання площі паралелограма у житті
Площа паралелограмаа не лише шкільна задача. Вона корисна у будівництві, архітектурі, дизайні, а також у фізиці. Наприклад, при обчисленні роботи сили чи площі ділянки землі.
Площа паралелограма у векторній формі

У старших класах і вищій математиці площу паралелограма знаходять через вектори:
S = |a × b|
де a і b — вектори, що утворюють паралелограм.
Історія вивчення площі паралелограма
Ще стародавні греки, зокрема Евклід, досліджували властивості паралелограма. Вони помітили, що площа цієї фігури схожа до площі прямокутника з такими ж основою та висотою.
Типові помилки при знаходженні площі паралелограма
Часто учні плутають основу з висотою, або ж використовують сторони без урахування кута між ними. Щоб уникнути помилок, важливо правильно малювати допоміжні елементи.
Як перевірити правильність обчислення площі паралелограма
Щоб переконатися у правильності результату, можна розбити паралелограм на два однакові трикутники. Якщо обчислити площу кожного трикутника і скласти, вийде та сама величина.
Площа паралелограма і інші геометричні фігури
Площа паралелограма пов’язана з площею прямокутника, ромба і квадрата. Усі ці фігури мають спільні властивості, але паралелограм є більш загальним випадком.
Задачі для закріплення теми площа паралелограма
- Знайти площу паралелограма, якщо a = 12 см, h = 7 см.
- Сторони дорівнюють 8 см і 15 см, кут між ними — 60°. Знайти площу.
- Діагоналі мають довжини 10 см і 14 см, а кут між ними — 90°. Обчислити площу.
Висновок про площу паралелограма
Площа паралелограма — це ключова тема геометрії, яка допомагає зрозуміти властивості площинних фігур. Вона може обчислюватися різними способами: через основу та висоту, через сторони і синус кута, або через діагоналі. Правильне використання формул дозволяє легко розв’язувати задачі.
Читати далі: Що таке відносна молекулярна маса – просто та зрозуміло
Часті запитання про площа паралелограма
Площа паралелограма — це числове значення, яке показує, яку частину площини займає ця фігура.
Основна формула: S = a × h, де a — основа, h — висота.
Так, можна. Для цього використовується формула S = a × b × sin(α).
Можна скористатися діагоналями або векторами, залежно від умов задачі.
Вона використовується в архітектурі, будівництві, фізиці та інших сферах.





